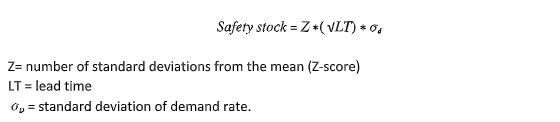Safety Stock Formulas & Calculation- The Ultimate Guide

• Inventory Management

Before we talk about the safety stock formulas and safety stock calculations, we need to understand the use of safety stocks.

Definition of Safety Stock

 

“Safety stock is carried to protect against the possibility of a stock out.”

 

Safety stock protects against these…

1. Customer Demand Variation, i.e. demand exceeds a sales forecast
2. Supplier Delivery Variation, i.e. supply deliveries are late than planned lead times.
3. Production Variation, i.e. production output is less than planned

In other words, it is the type of insurance policy to cover fluctuation in unpredicted and unforeseen events, whether sudden erratic demand, poor supplier delivery performance or force majeure.

 

One of my bosses used to say..

Safety stock is necessary evil….however, it is a waste! Must regularly review safety stock to minimize.

 

But reviewing safety stock is a time-consuming task, depending on the number of SKUs and what tools & software you are using.

To make it easy for you, we have used our experience and developed Inventory Optimization Tool, which can do days work in hours.

What you can get from this Inventory Optimization Tool is:

• The total cost of goods sold
• Current inventory had
• Planned Safety stock value
• Inventory Turns
• Days on Hand
• Current on-hand inventory (in $ value & % to total) grouped in coverage of months of stock available
• Inventory optimization proposals (A. Stock to stock with new safety stock levels; B. Stock to non-stock; C. Non-stock to non-stock; D. Non-stock to Stock with new SS levels)
• Current on-hand inventory profile in terms of (A. Usable inventory; B. Excess inventory; C. Obsolete Inventory)

 

Click here to access the tool and watch the complete step-by-step tutorial here.

 

 

Using adequate safety stock formulas are also must for any inventory planning methods you are using. Be it Kanban, MRP, Re-order Point and so on.

 

Disadvantages of Safety Stocks

 

While talking about safety stock calculations here, we must consider the disadvantages of high-safety stocks!

• High safety stock may cover the poor quality of manufacturing problems.
• It may also hide the supplier’s poor delivery performance
• High safety stock also hides inefficient production processes (long setup times, machine capacity issues, breakdown, etc.)
• It can also be a high skills shortage and inadequate manning
• In some cases, high safety stock hide transportation delays

 

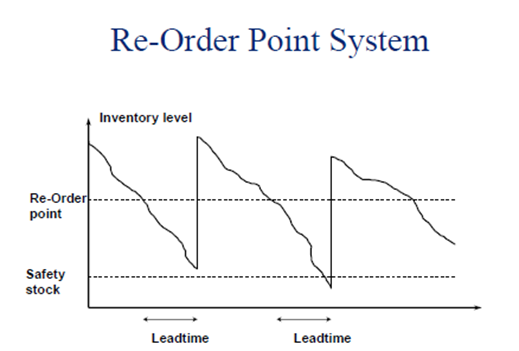
Role of Safety Stock in Re-Order Point Calculations

 

Reorder point can be considered to be a level of inventory when a new order is positioned with suppliers to procure added inventory, equaling the economic order amount. The reorder point comes as a signal that notifies businesses on when to place an order. In calculating the reorder point, you would need knowledge on the lead time between receipt and ordering of merchandise. This process may be influenced by the monthly supply or total dollar ceilings of the held or ordered inventory.

Reorder point is the metric that tells organizations two essential things:

• The right time to order more materials from your supplier(s); and
• The right time to produce more products by creating a Manufacturing Order

 

To calculate a reorder point with safety stock, multiply the average daily usage by the lead time and add the amount of safety stock you keep.

 

Re-Order Point =  Average Daily Sales × Lead time + Safety Stock

 

 

 

To understand the Characteristics of Re-order Point Systems, you can access Inventory Planning Methods – The Ultimate Guide

 

 

 

There are many ways in which to safety stock calculations are done and there are plenty of Safety Stock Formulas available which you could use. Below we will go through 7 different Safety Stock formula definitions to get a comprehensive figure for safety stock. Ultimately, we’ve given you a ‘bonus track’ of EOQ calculation!

 

Statistical Safety Stock Calculation

 

Safety stock should represent the supply side variation (covers the supplier delivery variation) plus the customer or production variation. Statistics can be used to calculate x % fill rate given the supply source’s specific demand variation and lead time.

Safety Stock Formula: Supply side variation + (Std. Dev. * service level desired * square root of the replenishment lead time)

 

Safety Stock Example

Given:

Supply-side variation = 2 days

Std. Dev. = 300

Demand per week = 500 (100/ day)

Desired service level = 99% or 2.33 Std. Dev.

Lead time is 5 weeks.

Calculate Safety stock…

 

Solution:     

Safety stock = 2 days (supply side variation) + (300 Std. Dev. * 2.33 desired service level * square root of 5)

Safety stock = 200 + 1563

Safety stock = 1763

 

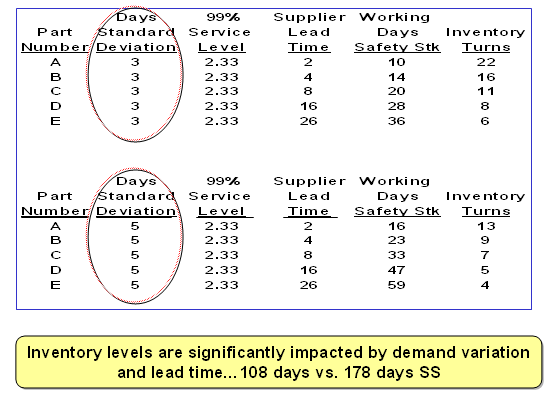
Demand Variation and Lead Time Impact

 

 

Other Available Safety Stock Formulas:

 

1.   Average SS

 

Safety stock = (max daily sale per unit * max LT in days) – (average daily sales per unit * average LT)

Although the above safety Stock formula is simple and gives an average amount of Safety Stock the company need to hold per unit of stock however does not take into account seasonal fluctuations (tradegecko, 2010)

 

2.   Heizer and Render (2013)

 

 

Although this approach takes into consideration standard deviation, it does not take account of time by including it as a variable in the equation (Emmanuel-Ebikake, 2015).

 

 

3.   Greasley (2013)

 

On the other hand, this approach takes account of lead time as a variable within the equation. This is one of favorite Safety Stock formula.

 

4.   King method

 

𝑆𝑎𝑓𝑒𝑡𝑦 𝑠𝑡𝑜𝑐𝑘 = 𝑍 ∗( √ 𝑃𝐶 / 𝑇1) ∗ 𝜎𝐷

 

Z= Z-score (a statistical figure based on the cycle service level) 

PC = performance cycle or total lead time (including transport time) 

T1 = time increment used for calculating standard deviation of demand 

𝜎𝐷 = standard deviation of demand

 

King (2011) safety stock formula, considers variations in demand, lead time, cycle time and fill rate. The purpose of the formula was to overcome the inaccuracies in data on demand. (Emmanuel-Ebikake, 2015)

5.   King (2011)

 

Safety stock = Z *√ ((PC/ T₁ * σ_D ²) + (σ_LT × D_avg)) ²

 

Z= Z-score (a statistical figure based on the cycle service level)

PC = performance cycle or total lead time (including transport time)

T₁ = time increment used for calculating standard deviation of demand

σ_D = standard deviation of demand

σ_LT = standard deviation of demand during the lead time

D_avg= average demand

.

This safety stock formula is used when demand and lead time variability are independent and are therefore influenced by different factors whilst still having normally distribution.

But when demand and lead time are not independent of each other, this equation changes to:

 

Safety stock = (Z *√( PC/ T₁ * σ_D) + ( Z * σ_LT * D_avg)

 

6 McKinsey & Company Method.

 

In selecting to consider any safety stock formula, it is important to consider the joint impact of demand and replenishment cycle variability. This can be accomplished by gathering valid samples of data on recent sales volume replenishment cycles. Once the data are gathered, it is possible to determine safety stock requirement using this safety stock formula:

 

σ_C = √R (σS² ) + S² (σR² )

 

σ_{C =} Units of safety stock need to satisfy 68 percent of all probabilities (one standard deviation)

R = Average replenishment cycle

σR = Standard deviation of the replenishment cycle

S = Average daily sales

σS = Standard deviation of daily sales

 

 

Summary:

 

Like many other statistical theories and a mathematical equation, no safety stock formula can be claimed to be best. Similarly, no formula can claim to be fit in all scenario. Use your knowledge and experience to find which formula best suits your business.

If you happen to know and used other safety stock formulas or safety stock calculations please do share in the comments box with me and the supply chain community.

 

 

Recommended Content in Inventory Management:

 

 

 

Recommended Course:

 

Frequently Asked Questions (FAQ)

How to calculate the safety stock?

To calculate safety stock, you typically follow these steps. First, determine the average demand during a specific time period. Next, calculate the standard deviation of the demand, which measures the variability. Multiply the standard deviation by a chosen Z-score (representing a level of confidence, e.g., Z=1.96 for 95% confidence), and finally, multiply this result by the square root of the lead time. Add the product to the average demand to obtain the safety stock level, acting as a buffer against uncertainties in demand and lead time.

What is an example of a safety stock?

An example of safety stock is when a retailer, based on historical sales data, anticipates an average demand of 100 units per week for a certain product. However, due to uncertainties such as unexpected spikes in customer demand or delays in supplier deliveries, they decide to maintain a safety stock of 20 units. This extra inventory acts as a buffer, ensuring that the retailer can meet customer demand even during unforeseen circumstances.

What is safety calculation?

Safety stock calculation involves assessing potential variations in demand and lead time to determine a buffer inventory level. It typically includes estimating average demand, calculating the standard deviation to measure variability, and factoring in a chosen confidence level (represented by a Z-score). The result, when added to the average demand, provides a safety stock level that helps mitigate the impact of uncertainties in supply chain dynamics.

What is minimum stock level?

The minimum stock level, also known as the reorder point, is the threshold at which the quantity of inventory triggers a reorder or replenishment process. It represents the minimum quantity of a product that should be on hand before new stock is ordered to prevent stockouts during the lead time required for procurement or production. The minimum stock level takes into account factors such as average demand, lead time, and safety stock to ensure that sufficient inventory is maintained to meet customer demand without disruptions.

References:

 

Heizer, J. and Render, B. (2014), Operations Management: sustainability and supply chain management, 11th ed. Pearson, England

Greasley, A. (2013). Operations Management, 3rd ed. Wiley, England

Slack, N.Brandon-Jones, A. Johnston, R. (2013) “Operations Management”  7th ed. Pearson, Harlow, UK

Robert Hammond of McKinsey and Company, Inc. as reported in Robert Fetter and Winston C. Dalleck Decision Models for Inventory Management (Burr Ridge, IL; Richard D, Irwin, 1961), pp. 105-8

Browne. J., Harhen. J. and Shivnan. J., (1996). Production Management Systems. 2nd editon. Addison Wesley. Harlow, England

DEBodt, M. and Van Wassenhove, L. 1983. “Lot sizes and safety stock in MRP”,  Production and Inventory Management, 24(1)